y
Positional Astronomy: <br>Annual parallax
Positional Astronomy:
Annual
parallax
{Note: If your browser does not distinguish
between "a,b" and "α, β" (the Greek letters
"alpha, beta")
then I am afraid you will not be able to make much sense of the
equations on this page.}
Geocentric or diurnal parallax varies
with the daily spinning of the Earth around its axis.
Annual
parallax is caused by the Earth's yearly orbit around the Sun.
The Earth shifts by 2a from side to side,
where a
is the radius of the Earth's orbit (assumed circular) = 1
Astronomical Unit.
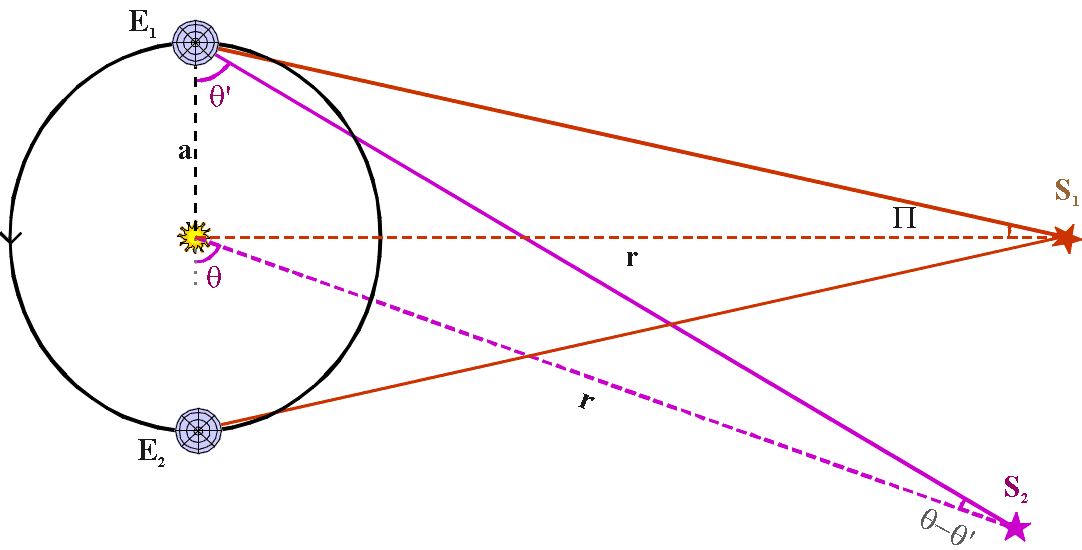
For the star S1, the maximum shift occurs
as the Earth moves from position E1 to E2.
If the distance between the Sun and the star S1 is r,
then we define the annual parallax as
Π,
where tan(Π) = a/r.
And
since a/r is always extremely small,
we may write Π
= a/r (in radians).
If the star is not at S1, but at some
other arbitrary position S2,
then the shift in
position as Earth moves from E1 to E2 will
appear less.
Let the direction from the Sun to the star make an
angle θ
with the line E1E2
.
But the star appears at angle θ'
from Earth at E1.
By plane trigonometry,
sin(θ-θ')/a
= sin(θ')/r
so
sin(θ-θ')
= sin(θ')
a/r
=
sin(θ') sin(Π)
Since (θ-θ')
is a very small angle,
we can replace θ'
by θ, and write
θ-θ'
= Π sin(θ)
The apparent shift is towards the Sun,
and
it alters the star's ecliptic longitude λ
(so this is another occasion for using ecliptic coordinates).
If
the star is not in the plane of the ecliptic,
there is a shift in
ecliptic latitude β too.


The star X at (λ, β)
is shifted to X' at (λ+Δλ, β+Δβ)
along a great circle arc towards the position of the Sun S.
XX' is the parallactic shift Π sin(θ).
We need to find the shifts Δλ and
Δβ.
UX is the arc of a small circle centred on the
ecliptic pole K,
passing through the star X.
The length of arc UX is Δλ cos(β) – the shift
in
longitude.
The length of arc UX' is -Δβ – the shift in latitude.
Consider the tiny triangle UXX' as a plane
right-angled triangle,
and denote the angle at X by the arbitrary symbol ψ:
UX = XX' cos(ψ) = Π sin(θ) cos(ψ)
UX' = XX' sin(ψ) = Π sin(θ) sin(ψ)
In other words,
Δλ cos(β) = Π sin(θ)
cos(ψ)
Δβ = -Π sin(θ) sin(ψ)
(equations 1)
To eliminate θ and ψ from these two equations,
we
use the spherical triangle KXS.
First, by the sine rule:
sin(90°+ψ/sin(90°) =
sin(λS-λ)/sin(θ)
i.e. sin(θ) cos(ψ) =
sin(λS-λ)
(expression
2)
where λS is the ecliptic longitude of the
Sun.
Then, by the cosine rule:
cos(90°) = cos(θ) cos(90°-β) + sin(θ)
sin(90°-β) cos(90°+ψ)
i.e. 0 = cos(θ) sin(β) - sin(θ) cos(β)
sin(ψ)
So: sin(θ) sin(ψ) = cos(θ)
sin(β)/cos(β)
To get rid of the cos(θ) on the right-hand side of
this expression,
we use the cosine rule again:
cos(θ) = cos(90°-β) cos(90°) + sin(90°-β)
sin(90°) cos(λS-λ)
i.e. cos(θ) = cos(β) cos(λS-λ)
Substituting this expression for cos(θ)
in the previous equation:
sin(θ) sin(ψ) = cos(β)
cos(λS-λ) sin(β) /cos(β)
i.e. sin(θ) sin(ψ) =
cos(λS-λ) sin(β)
(expression 3)
Now we can substitute these expressions (2)
and (3) in equations (1),
to get:
Δλ cos(β) = Π
sin(λS-λ)
Δβ
= Π cos(λS-λ)
sin(β)
This is actually the formula for an ellipse,
of the form:
x = a cos(θ), y = b sin(θ)
where x is the
shift parallel to the ecliptic [ Δλ cos(β) ]
y is the
shift perpendicular to
the ecliptic [ Δβ ]
and θ is temporary shorthand
for [ 90° - (λS-λ) ].
So we have a = Π and b = Π sin(β)
In other words, this parallactic ellipse has
semi-major axis Π, parallel to the ecliptic,
and semi-minor axis Π sin(β), perpendicular to the ecliptic.
So, during the year,
the star appears to trace out a parallactic ellipse,
which is a reflection of the Earth's orbit.
For a star on the ecliptic (β = 0°) it reduces to a straight
line;
for a star at the pole of the ecliptic (β = 90°) it becomes a
circle.
The size of a star's parallactic ellipse
yields its distance,
in units of parsecs (parallax-seconds):
r (in parsecs)
= 1 / Π
(in arc-seconds),
so a star at 1 parsec would have parallax Π = 1 arc-second.
(In fact, no star is this close.)
Exercise:
A star’s true position is
Right Ascension 6h 0m 0s, declination 0° 0' 0",
and
it lies at a distance of 25 parsecs.
On the date of the Spring
Equinox,
how far will it appear to be shifted by annual parallax,
and in what direction?
Click here
for the answer.
Previous section:
Geocentric
parallax
Next section: Aberration
Return to index