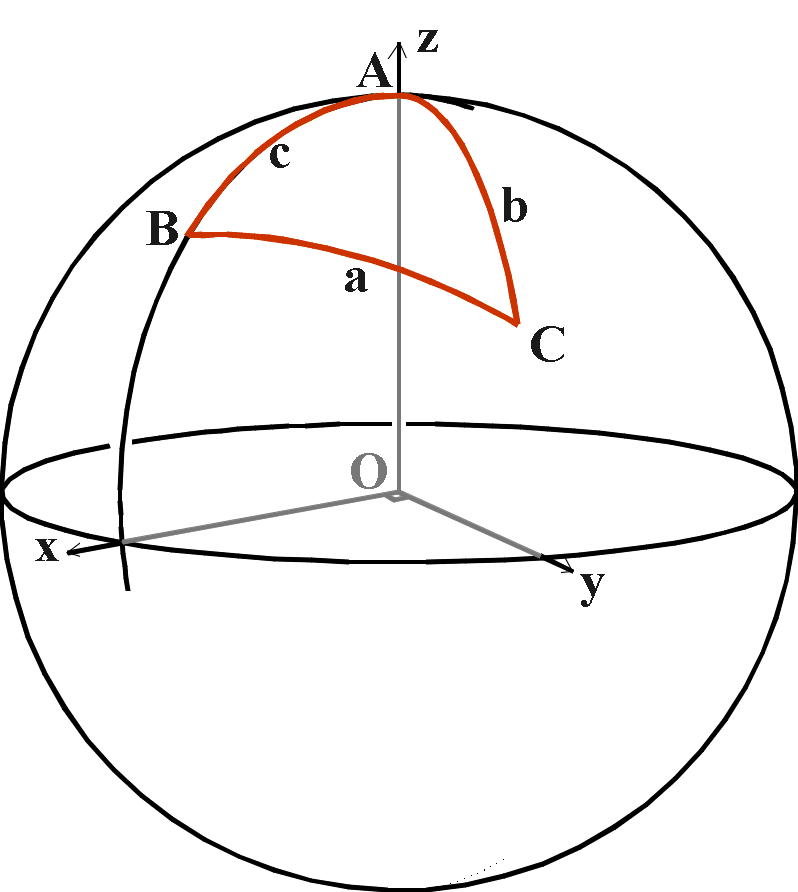
 Consider
a triangle ABC on the surface of a sphere with radius = 1.
Consider
a triangle ABC on the surface of a sphere with radius = 1.
A great-circle arc, on the sphere, is the analogue of a straight line, on the plane.
Where two such arcs intersect, we can define the
spherical angle
either as angle between the
tangents to the two arcs, at the point of intersection,
or
as the angle between the planes of the two great circles where they
intersect at the centre of the sphere.
(Spherical angle is only
defined where arcs of great circles meet.)
A spherical triangle is made up of three arcs
of great circles, all less than 180°.
The sum of the angles
is not fixed, but will always be greater than 180°.
If any
side of the triangle is exactly 90°, the triangle is called
quadrantal.
There are many formulae relating the sides and angles
of a spherical triangle.
In this course we use only two: the sine
rule and the cosine rule.
 Consider
a triangle ABC on the surface of a sphere with radius = 1.
Consider
a triangle ABC on the surface of a sphere with radius = 1.
(See note)
We use the capital letters A, B, C to denote the
angles at these corners;
we use the lower-case letters a, b, c to
denote the opposite sides.
(Remember that, in spherical
geometry, the side of a triangle is the arc of a great circle,
so
it is also an angle.)
Turn the sphere so that A is at the "north
pole",
and let arc AB define the "prime meridian".
Set up a system of rectangular axes OXYZ:
O is at
the centre of the sphere;
OZ passes through A;
OX passes
through arc AB (or the extension of it);
OY is perpendicular to
both.
Find the coordinates of C in this system:
x
= sin(b) cos(A)
y = sin(b) sin(A)
z = cos(b)
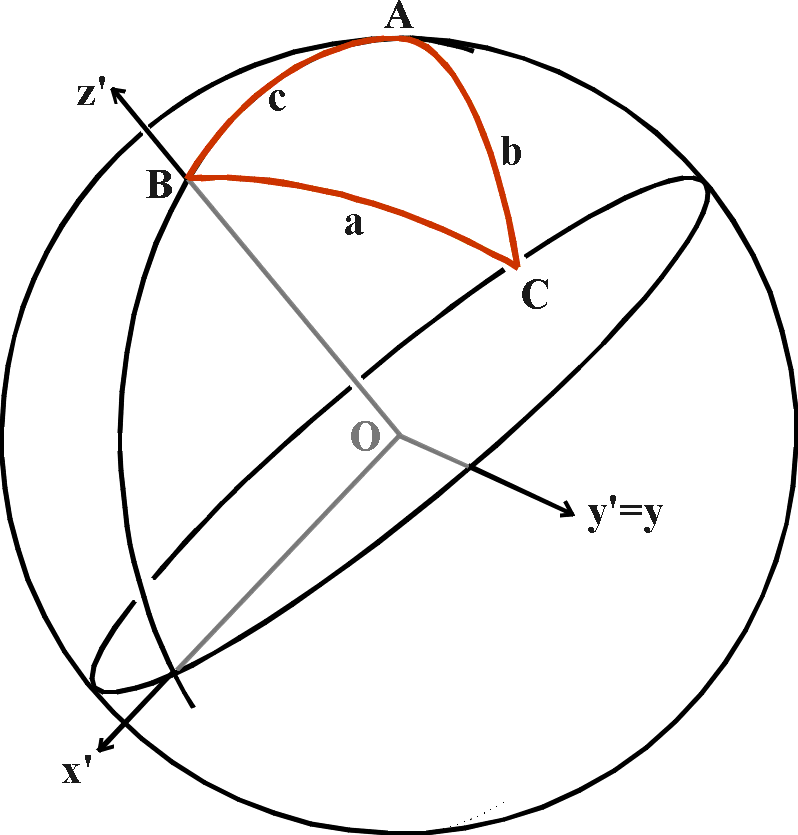
Now
create a new set of axes,
keeping the y-axis fixed and moving the
"pole" from A to B
(i.e. rotating the x,y-plane through
angle c).
The new coordinates of C are
x'
= sin(a) cos(180-B) = - sin(a) cos(B)
y' = sin(a) sin(180-B) =
sin(a) sin(B)
z' = cos(a)
The relation
between the old and new systems
is simply a rotation of the
x,z-axes through angle c:
x' = x cos(c) - z
sin(c)
y' = y
z' = x sin(c) + z cos(c)
That is:
- sin(a) cos(B) =
sin(b) cos(A) cos(c) - cos(b) sin(c)
sin(a) sin(B) =
sin(b) sin(A)
cos(a)
= sin(b) cos(A) sin(c) + cos(b) cos(c)
These three equations give us the formulae for solving spherical triangles.
The first equation is the transposed cosine rule,
which is sometimes useful but need not be memorised.
The second equation gives the sine rule.
Rearrange as:
sin(a)/sin(A)
= sin(b)/sin(B)
Similarly,
sin(b)/sin(B)
= sin(c)/sin(C), etc.
So the sine rule is usually expressed
as:
sin(a)/sin(A) = sin(b)/sin(B) =
sin(c)/sin(C)
The third equation gives the cosine rule:
cos(a) = cos(b) cos(c) + sin(b) sin(c)
cos(A)
and similarly:
cos(b) =
cos(c) cos(a) + sin(c) sin(a) cos(B)
cos(c)
= cos(a) cos(b) + sin(a) sin(b) cos(C)
Here they are together:
sine
rule:
sin(a)/sin(A) = sin(b)/sin(B) =
sin(c)/sin(C)
cosine rule:
cos(a)
= cos(b) cos(c) + sin(b) sin(c) cos(A)
cos(b)
= cos(c) cos(a) + sin(c) sin(a) cos(B)
cos(c)
= cos(a) cos(b) + sin(a) sin(b) cos(C)
The cosine rule will solve almost any triangle if it
is applied often enough.
The sine rule is simpler to remember but
not always applicable.
Note that both formulae can suffer from
ambiguity:
E.g. if the sine rule yields
sin(x)
= 0.5,
then x may be 30° or 150°.
Or, if the
cosine rule yields
cos(x) = 0.5,
then x may
be 60° or 300° (-60°).
In this case, there is
no ambiguity if x is a side of the triangle, as it must be
less than 180°,
but there could still be uncertainty if an
angle of the triangle was positive or negative.
So, when applying either formula, check to see if the
answer is sensible.
If in doubt, recalculate using the other
formula, as a check.
Exercise:
Alderney,
in the Channel Islands, has longitude 2°W, latitude 50°N.
Winnipeg, in Canada, has longitude 97°W, latitude 50°N.
How far apart are they, in nautical miles, along a great-circle
arc?
If you set off from Alderney on a great-circle route to
Winnipeg,
in what direction (towards what azimuth) would you
head?
Click here for the answer.
Previous section: The
terrestrial sphere
Next section: Coordinate
systems: the horizontal or "alt-az" system
Return
to index